What every layperson should know about Feynman diagrams
- Yahya Ashraf

- Sep 26, 2021
- 4 min read
Updated: Nov 14, 2022
Every so often, a scientist is born who is so brilliant and so charming that they become a cultural icon. Here I am talking about Richard P. Feynman, who is definitely one of the coolest scientists of the 20th century.
While stories abound of his interest in picking locks and his fondness for having a good time, it is in the realm of understanding the quantum nature of matter and energy that he made his real impact. In this article, we talk specifically about his contribution to how modern physicists calculate how particles scatter.
Now Feynman can’t take all the credit. He shared his Nobel Prize with Julian Schwinger and Sin-Itiro Tomonaga, but those two guys were all about really intense equations. Feynman’s real genius was the way in which he made the whole process intuitive. He made it so that anyone who can doodle can at least start the process of calculating what happens inside a high energy particle collision.
Feynman diagrams are easy to write and easy to understand, at least at the most basic level. For example, let’s talk about the simplest particle collision imaginable when two electrons bounce off one another.
Classically, we’d calculate this process using the electric field and considerations like conservation of energy or just a smidge of calculus. However, in the quantum world, we need to remember that not only do electrons come in discrete chunks, but so do photons. In fact, a form of photons makes up the electric field. So maybe when two electrons scatter, they do so by two electrons approaching one another and then one of them emits a photon which then hits the other electron. Both electrons recoil using the standard energy and momentum physics you might have encountered in school.
So we can draw the Feynman diagram that does precisely that. Two electrons exchanging a photon.
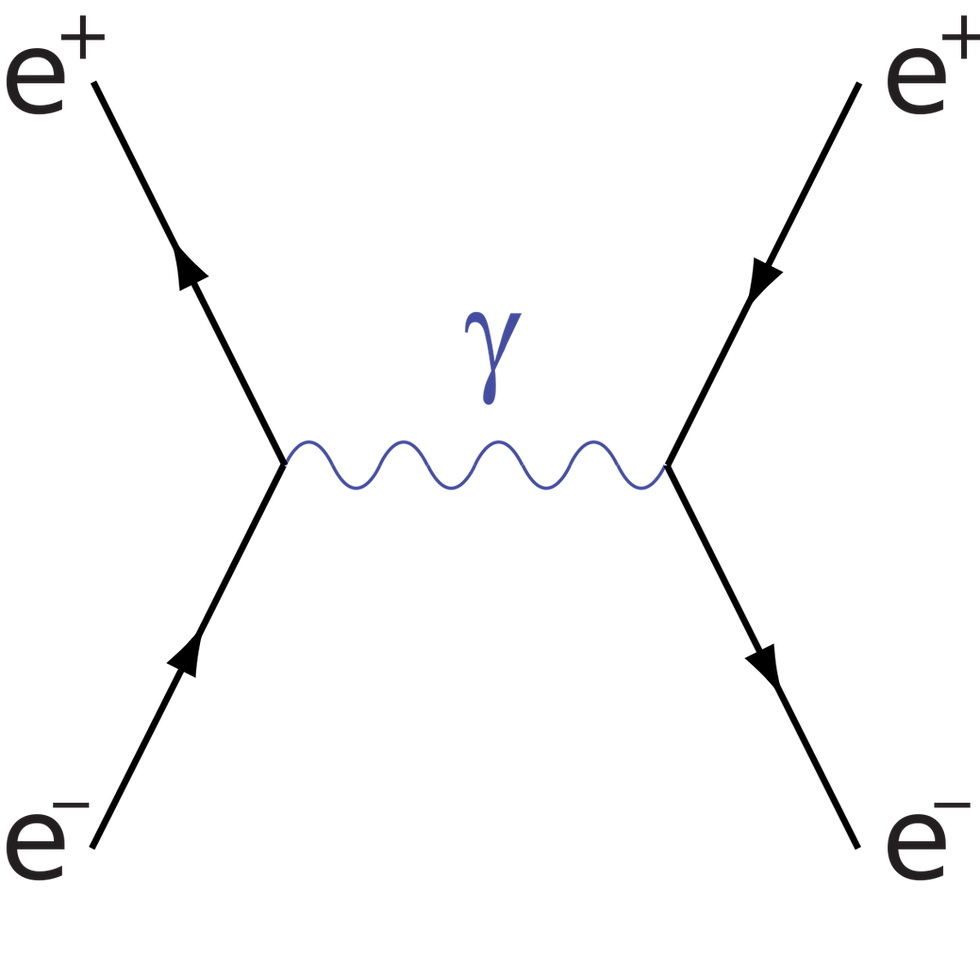
We’re going to focus on this particular Feynman diagram, but you should know that there are others. For instance, another way in which two electrons can scatter might be that one of the electrons might also emit an additional photon, either before the “big scatter” or after. There are other options. For instance, maybe one of the electrons could emit a second photon that is absorbed by the other electron. Or maybe an electron could emit a photon that it then reabsorbs. Or maybe as the photon moves from one electron to another, it might temporarily turn into an electron/positron pair before it recoalesces into a photon to complete the scatter.
Or, we could imagine something even crazier still, with multiple photons being exchanged, with some of them creating other particles and the photons interacting with the temporary particles. There are tons of possible combinations of particles and the result is the same basic outcome, which is that two electrons scatter.
While all things could happen, it turns out that each time a photon interacts with a charged particle, the chance that this happens is less and less likely. And that’s a big effect. A single extra photon emission drops the probability to 1%, while two emitted photons drops the probability to 1% of 1%. So really only the one simplest Feynman diagram is truly important. And this is a crucial point. The single-photon exchange is the dominant contribution and only for very precise calculations do you need to take into account the other diagrams. So let’s return to the case of a single photon exchange. So what does that picture tell us? Well, I’m gonna say something that might just blow your mind. The picture is really… an equation! Now, to understand that, I’m going to guide you through the pieces, starting with the vocabulary.

Each symbol in the picture corresponds to a piece of an equation. For instance, the incoming electron corresponds to the letter I, while the outgoing electron corresponds to the letter O. The photon corresponds to a fraction, specifically -igμv over p-squared. The i is the square root of negative 1, while the g-sub-mu-nu is used to handle adding up all the relevant subatomic spin for the photon. The p is just the energy carried by the photon.
A vertex has its own corresponding mathematical term, which is an i e gamma, where the superscript mu or nu doesn’t mean power like square or cube. Instead, it has some implied information on how to add everything up and is related to the subscripts in the g from the photon.
So now we’re ready to stitch things together. We can draw the simple Feynman diagrams and immediately write down a corresponding equation. Check it out. See how each piece fits in. I’ve colour coded the symbols and the figures so you can see how they come together.
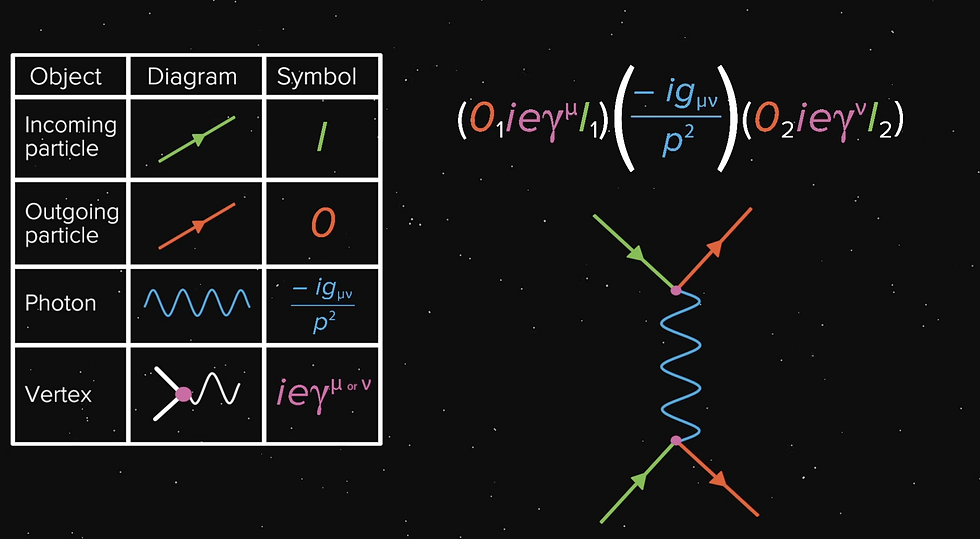
Now actually solving that equation is pretty hard but the real message and the real genius of Feynman diagrams are that each drawing has a corresponding equation. So you first have to imagine all the possible pictures, and then the equations come more or less for free.
When you get right down to it, the whole idea is pretty amazing.




Brilliant